
Game theory is used to by mathematicians to calculate the best course of action to take in various strategic situations. At its most complex game theory can be used, not only by businesses and economists, but also social scientists, psychologists, philosophers and biologists. At its simplest, it’s something we can all make use of in our everyday lives.
What Is Game Theory?
Whilst game theory has many different forms depending on the situation it is applied to, it is easiest to explain by giving a basic example of how it works, such as the well known prisoner’s dilemma;
Imagine that you and a friend have been arrested by the police force of a corrupt government, accused of a joint crime. They are assuming that you are guilty and there will be no trial. Instead, they offer you two options; deny the charges or confess to them.
The possible outcomes of your decision are;
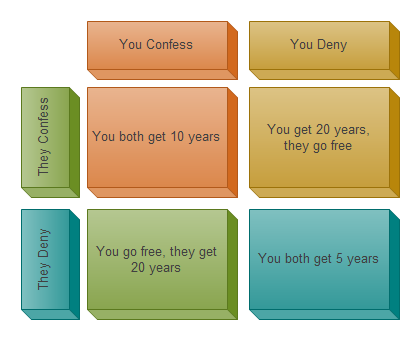
- If you both confess, you’ll both get 10 years in jail.
- If you confess the charges and your friend denies them, he’ll get a full 20 years, but you’ll be rewarded for exposing him by going free (and vice versa.)
- If, even in the face of this offer, you still both deny the charges, they will entertain the idea that you are innocent after all and only give you five years each, just in case.
You are held in separate cells and can’t communicate.
The situation and its possible outcomes can be expressed in a matrix like this;
If you think they will deny, it is best to confess. That way you go free instead of getting 5 years for denying it along with them.
However, even if you think they will confess, it is still better for you to confess as well. That way you’ll only get 10 years, avoiding the 20 years you’d get if you choose to deny the charge.
As, no matter what the other person does, it is better for you to confess, confession is what’s called the ‘dominant’ strategy.
So, with that in mind maybe it’s not a dilemma at all? Surely it is best just to confess, isn’t it?
Nash Equilibrium
This situation is what’s called a ‘Nash equilibrium’ (named after the pioneering mathematician John Nash, played by Russell Crowe in the film ‘A Beautiful Mind’).
In a ‘Nash equilibrium’ one person looks at what the other might do and decides that, as they can’t tell what their choice will be, they have to stick with the option that is safest in all cases. They have to go for the ‘dominant’ strategy. This applies to both prisoners, hence the state of equilibrium.
But is this actually what’s best for the people involved? No, it isn’t!
Why? Look again at the prisoner’s dilemma example above. Because both prisoners will reach that same conclusion that confession is the ‘dominant strategy’ both will confess. That means they both get 10 years in jail.
However, if they both deny they only get 5 years! This is the option that involves the least combined jail time. On top of that the jail time is split fairly between both parties. This makes it what’s called the ‘optimum outcome’. In other words, it’s the best thing that could happen, overall.
But can you trust your partner to figure this out? If you deny and they still confess you’re looking at 20 years!
In real life people, especially when it comes to businesses, tend to see others as competition rather than partners. Therefore, they go for the safe option i.e. the dominant strategy.
The real lesson of ‘Nash equilibrium’ is that, due to not cooperating properly people and businesses usually miss out on the ‘optimum outcome’ because they are scared of straying from the ‘dominant’ option, which guards against the unpredictability of others.
Basically, we could all be better off if we all worked together, but in business that isn’t how it works.
How Do Businesses Use Game Theory?
The way that businesses decide on their pricing structures is very similar to the logic of the prisoner’s dilemma.
When a business sets a pricing strategy it has two basic options;
- Charge as much as possible, making maximum profit from each sale.
- Charge as little as possible, keeping prices down and driving up demand.
These are the two extremes of the scale and all pricing strategies fall between these two poles. But if this is the case, why do similar products generally cost more or less the same? Why don’t we see a wider variety of pricing structures used?
The answer lies with the Nash Equilibrium.
In our earlier example we saw that if each prisoner denied the charge it would produce the ‘optimum outcome’ but that they would also run the risk of going down for 20 years if their partner confessed.
For two similar competing businesses the optimum outcome would be if they both set high prices, as they would make high profits on each sale and, as customers would have little reason to pick one over the other, prices being the same, they would likely have an equal market share.
However, if one business sets its prices at an artificially high level, they have no guarantee that other businesses will do the same. They run the risk of competitors undercutting them.
Should this happen the business with the lower price will take a huge chunk of the market share, as customers will choose the cheaper option. The firm with lower prices will prosper and the firm with high prices will be ruined.
By this logic, if one firm finds itself in a position where it can offer extremely low prices, all the other firms are forced to lower theirs as well, to avoid losing custom. This will eat into their profits and make all the businesses worse off.
(Some businesses have even used this as a tactic to ruin their competition. Some big chain stores have been known to move into an area, lower prices to the point that they are making a negative ROI, forcing others to do the same. The local businesses can only survive making a loss for a while, but the chain store can go on, as it is supported by the profits from other branches. Once all the local competition has been eliminated the chain store puts up its prices, knowing customers have no choices left!)
As a result, competing businesses are held in a sort of ‘Nash equilibrium’ when it comes to pricing, going for a competitive price to avoid being undercut, but also trying to avoid triggering a ‘race to the bottom’ that makes everyone worse off. This is good news for customers as it means they usually get a decent deal.
If the businesses were to get together and cooperate to keep prices high it would be very harmful to consumers. Some businesses attempt to do this, forming cartels and making agreements with each other. In most countries and in most industries this practice of ‘price fixing’ is illegal.
In the same way that the prisoners were held in separate cells to stop them cooperating with each other, government’s encourage businesses to be competitive so that they will not indulge in price fixing.
How Can I use These Ideas to Improve My Personal Finances?
There are a number of ways you can use a good knowledge of game theory to improve your finances. For one thing, simply being aware of how ‘Nash equilibrium’ should keep prices low will help you spot when businesses are not behaving in a competitive manner and avoid getting ripped off.
Sometimes you can even use game theory to save money by forcing businesses into a sort of prisoner’s dilemma which will make them more competitive and thus lower their prices.
For example, one leading thinker in the area of game theory uses this technique whenever he buys a car;
In the morning he will phone every dealership within easy travelling distance of his home. He tells them all the same thing; that he has decided that he will definitely be buying X car that day at 5pm. He will turn up with a cheque at whichever dealership phones back with the best offer in the mean time.
In doing so, he creates a sort of reverse bidding war. As we’ve seen it would be best for all the dealerships involved if they all ignored him, as they wouldn’t have to lower their price. But by now we know that businesses rarely go for the ‘optimum outcome’. Instead, they’ll go for the ‘dominant strategy’ and lower their price to avoid losing an easy sale, assuming the other show rooms are doing the same thing. The gentleman in question claims to have thousands using this method.
Of course sometimes, even though you are a private individual rather than a business you yourself may have to use game theory in an uncooperative manner, for the sake of your personal finances.
For example, if you are bidding on a house game theory can be very useful in helping you decide how much you’d like to bid. If you are competing with another person to get the house the ‘optimum outcome’ as far as you’re concerned would be if you both put in low bids. One of you is going to win the house anyway, so why go crazy?
However, you aren’t going to be discussing your bids with the other interested party (you probably won’t know who they are) and you have to assume that if you go with a low bid they might outbid you. By the same token, if you are desperate to avoid being outbid and put in a higher offer, you may end up paying several thousand pounds more than need be.
In this case you will both go for the middle path, trying to avoid being outbid on the one hand, and paying more than need be on the other. This is the best that you can do, given what others may be doing. In other words, it is the ‘dominant strategy’.
This is especially true if you are buying a house in Scotland, as you will normally make a sealed bid for it. In this case you only get one chance to make a choice on how much to offer and you have no way of knowing what the other interested parties might do. This makes it highly analogous with the prisoner’s dilemma we have been looking at.
In England houses are sold in a slightly different style similar to that of an traditional English auction, where even if the other bidder out bids you, the auctioneer will come back to you and give you the chance to put in a higher offer.
In this instance, the fact that you will get multiple chances to bid and the fact that you will be aware of what your fellow bidders are doing means that it may be easier for you to co-operate and reach an ‘optimum outcome’ by only increasing your bids by a small amount each time.
You can also use you knowledge of game theory to undo the ‘Nash equilibrium’ in situations where you and your friends are going for a ‘dominant strategy’ when you could get an ‘optimum outcome’ instead.
When you think about it, there are a lot of situations that may arise in your social life that are similar to the prisoner’s dilemma.
For example, when you and a group of friends are going out to a social event you, like a business, have to pick a sort of pricing strategy. Do you go somewhere expensive, that will be a really great experience, but maybe a bit expensive for some people in the group, or do you go somewhere that everyone can easily afford, but maybe be less enjoyable?
As people are often embarrassed in discussing matters of personal finance they go for what appears to be the ‘dominant option’ of picking something that is a slight strain on their finances, but that they think everybody else will want to do.
However, unlike businesses and prisoners, there are no rules to stop you and your friends communicating with each other to discover the optimum solution. You may all be worried about suggesting somewhere cheap and risking embarrassment, but if you come out and say it you’ll probably find everyone was thinking the same thing, they just didn’t say so based on what that thought the rest of the group would want. In other words, they were stuck in an unhelpful ‘Nash equilibrium’.
If you know your stuff you can avoid such situations!
